
Un libro de divulgación de lógica presenta una versión del sistema de deducción natural de Gentzen con las reglas siguientes:

(Garrido, M., (1991), Lógica Simbólica, Madrid: Tecnos, p. 84).
Más adelante, en el mismo texto, se presentan las siguientes "leyes":
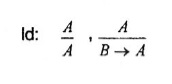
con las siguientes "fundamentaciones":

Es el propósito del presente escrito sugerir, con propósitos didácticos, un sistema de reglas diferente del de Garrido y, al mismo tiempo, efectuar algunos comentarios sobre las "leyes" y "fundamentaciones" presentadas.
1. En primer lugar, sugerimos el siguiente juego de reglas en el siguiente orden (¡que ya está presente en Gentzen!):
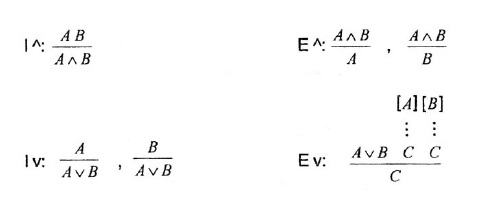
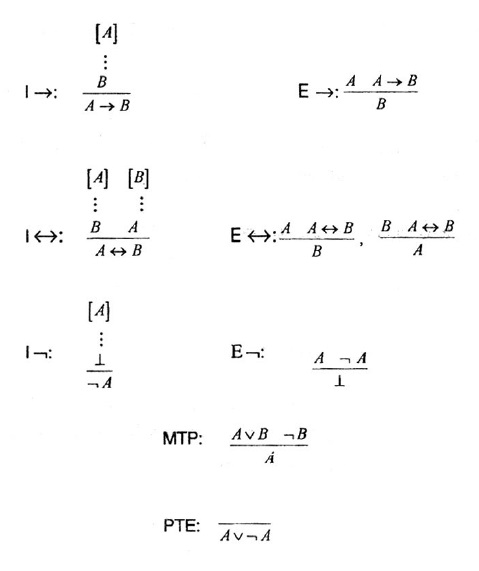
Consideramos que esta versión es mejor, por lo menos, por las siguientes razones:
a) permite DISTINGUIR, desde un comienzo, los conceptos de lógica minimal, intuicionista y clásica (consideramos que esto es de importancia lógica, matemática, filosófica y didáctica). El sistema de Garrido no permite definir a la lógica intuicionista, dado que el agregado de la regla DN a las demás produce la lógica clásica a partir de la minimal;
b) para la lógica minimal, el sistema goza de una simetría completa:
se dispone, para cada símbolo lógico (con excepción de
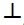 ), de una regla de introducción y otra de eliminación;
), de una regla de introducción y otra de eliminación;
c) la regla MTP es más intuitiva que la regla original de Gentzen:
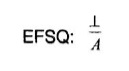
La regla EFSQ puede ser más útil que MTP en el estudio metateórico, pero MTP expresa formalmente la idea intuitiva de descarte;
d) tanto las derivaciones de la regla DN como las de

a partir de la regla PTE, tienen menos pasos y son más intuitivas que las derivaciones de PTE a partir de las reglas DN o Absurdo Clásico. Por ejemplo, con nuestro sistema de reglas, la regla Absurdo Clásico se deriva así:
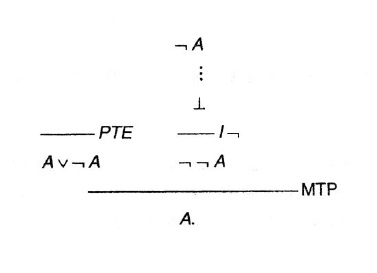
e) la regla MTP es independiente de PTE, pero no lo es ni de DN ni de Absurdo
Clásico;
f) históricamente PTE parece más importante.
2. Creemos más conveniente el uso de árboles en lugar de proceder de forma lineal. Gentzen trabajó con árboles y así siguió casi toda la tradición de teoría de la prueba. El único posible inconveniente de los árboles es que hay que reescribir las fórmulas cada vez que se las usa.
3. En relación a las "leyes" y "fundamentaciones" presentadas, nos parece pertinente expresar que no hay menester de la ley Id de Garrido, pues habitualmente se define el concepto de derivación de tal forma que una fórmula es considerada una derivación de ella misma. Por ejemplo,
p
es una derivación de p a partir del conjunto {p}, esto es, la fórmula p prueba que {p} ├ p.
4. En relación a la derivación
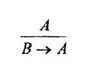
al autor también le parece pertinente expresar que habitualmente ella se considera como un caso particular de la regla de introducción del condicional:
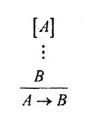
Es
decir, si disponemos de A, podemos obtener, en un sólo paso, B
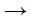 A
por
medio de la regla mencionada. Dicho sea de paso, la forma de derivar
la fórmula A
A
por
medio de la regla mencionada. Dicho sea de paso, la forma de derivar
la fórmula A
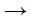 A
es
la siguiente:
A
es
la siguiente:
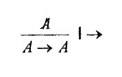
Esto evita los rodeos de la "fundamentaciones" de Garrido, cuestión que los lógicos han estudiado de manera sistemática obteniendo resultados sobre la posibilidad de derivaciones sin rodeos.
5.
Pensamos que es muy conveniente incorporar el uso del simbolo 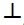 para
indicar el concepto de contradicción, pues simplifica algunas
derivaciones (Gentzen también trabajó con dicho
símbolo). Por ejemplo, a la siguiente derivación de
para
indicar el concepto de contradicción, pues simplifica algunas
derivaciones (Gentzen también trabajó con dicho
símbolo). Por ejemplo, a la siguiente derivación de 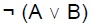 a partir de
a partir de 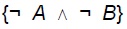 habría que agregarle un rodeo para que fuera adecuada a la
regla de eliminación de la disyunción:
habría que agregarle un rodeo para que fuera adecuada a la
regla de eliminación de la disyunción:
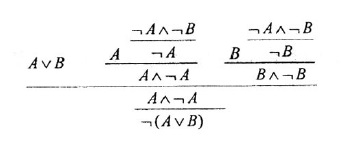
6. Comparación con Gentzen: en relación a dicho autor, los únicos cambios introducidos son el de substituir la regla
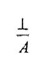
por
MTP, y el de agregar el conectivo 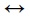 con sus dos reglas, aunque sea
(minimalmente)
definible a partir de
con sus dos reglas, aunque sea
(minimalmente)
definible a partir de 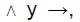 porque, desde un punto de vista
didáctico, creemos más conveniente no tener una actitud
reduccionista.
porque, desde un punto de vista
didáctico, creemos más conveniente no tener una actitud
reduccionista.
Esta obra está bajo licencia
Creative Commons Atribución-NoComercial-SinDerivadas 2.5 Argentina