A entonces Γ ∪{B} Δ Monotonía UNLP; UBA
Resumen
Frank Ramsey (1931) estableció ciertas condiciones que deberían cumplirse a
fin de evaluar las proposiciones condicionales, conocidas hoy como Test de Ramsey
(TR) En este trabajo se muestra que las teorías sobre condicionales contrafácticos
de Chisholmj, Stalnaker y D. Lewis, satisfacen el TR y la incompatibilidad de
TR con la Teoría de la revisión de creencias (AGM). En la última sección se
analiza el comportamiento del TR en la propuesta de G. Grocco y L. Fariñas del
Cerro, basada en una generalización del cálculo de Secuentes pero introduciendo
la novedad de secuencias auxiliares cuya noción de consecuencia es no-monótona.
Abstract
Frank P. Ramsey, (1931), stated certain conditions that should occur in order
to evaluate conditional propositions, known today as Ramsey Test (RT). In this
paper it is shown the satisfactibility of TR in the theories on contrafactual
conditionals of Chisholm, Stalnaker and D.Lewis and the incompatibility of the
TR with the Theory of Belief Revision (AGM). The last section is appointed to
analyze the behavior of the TR in the proposal of G.Grocco and L. Fariñas del
Cerro, based on a generalization of Sequent Calculus to the logic of contrafactual,
introducing the novel idea of auxiliary sequences whose notion of consequence
is not monotonic.
En 1931, después de su temprana muerte, R. B. Braithwhite edita los trabajos de Frank P. Ramsey, bajo el título The Foundations of Mathematics and other Logical Essays. 1 Principalmente en dos de ellos, Truth and Probability y General Proposition and Causality aventura ciertas ideas acerca de la naturaleza de la lógica y de cómo evaluar los enunciados hipotéticos (variable hypotheticals, o, en terminología actual, los enunciados condicionales. La influencia de sus trabajos no fue inmediata y es posible afirmar que sus ideas toman vigencia recién a partir de 1946 con los trabajos de R. Chisholm de N.Goodman acerca de la conexión entre leyes científicas y enunciados condicionales. En efecto, es precisamente una referencia incompleta de Chisholm a una nota que aparece al pié de la página 247 del artículo de Ramsey, General Proposition and Causality, que la que originó el hoy conocido como Test deRamsey (TR). En forma completa la nota dice:
(a) "(...) Si dos personas están discutiendo acerca de "Si p entonces q" y ambas están en duda frente a "p", entonces están añadiendo hipotéticamente "p" a su conjunto de conocimiento y argumentando sobre esa base acerca de "q"; de tal forma que, en un sentido, "Si p, q" y "Si p,¬ q, son contradictorios. Podemos decir que ellas están ajustando sus grados de creencia en q dado p. Si p resulta ser falso, estos grados de creencia se vuelven nulos (...)" (1931, p.247, nota a pie) En la página siguiente completa su idea con la siguiente afirmación forma:(b) (...) "En general podemos afirmar junto con Mill, que la afirmación "Si p entonces q" significa " q es inferible a partir de p", esto es, por supuesto, a partir de p junto con ciertos hechos y leyes no afirmados pero de cierta forma indicados por el contexto. Esto significa que p→q se sigue de estos hechos y leyes (...)" (1931, p.248)
Los párrafos (a) y (b) han sugerido distintas perspectivas de análisis.Según nuestra opinión, de lo afirmado en a) y/o b) se infieren, al menos, las siguientes características:
(i) La evaluación de un enunciado condicional debe darse en términos del grado de creencia en el consecuente, dado el antecedente.
(ii) La expresión si p entonces q debe entenderse como significando q se deduce de p en conjunción con un conjunto Γ de creencias (hechos o leyes) fijado por el contexto.
(iii) Sobre la base de aceptar Γ, deducir el condicional material p→ q
(i) reafirma el carácter epistemológico sostenido por Ramsey en Truth and Probability acerca de que la lógica del pensamiento humano no es la lógica formal (o de la consistencia), sino que incluso puede llegar a diferenciarse de ella. En tanto tal, ella no es un conjunto de verdades necesarias, sino que habla sobre conocimientos probables o creencias. De esto podría deducirse entonces que, para Ramsey, no podría darse para los enunciados condicionales un tratamiento lógico clásico. Sin embargo, las cláusulas (ii) y (iii) parecen indicar que, en ciertas condiciones, ellos pueden reducirse a condicionales clásicos.
Siguiendo esta línea de pensamiento, Chisholm, en The Contrary to fact Conditionals de 1946 y Goodman en The Problem of Counterfactual Conditionals de 1947, proponen la hoy conocida como Teoría de la Derivabilidad, donde se establecen las condiciones de verdad para un condicional contrafáctico. Expresadas en terminología moderna, esta dice:
Si A entonces B es aceptado/verdadero sii {A} ∪ Γ ├ B
En palabras, el enunciado A entonces B debe ser evaluado en tanto inferencia de B a partir de A en unión con un conjunto de enunciados Γ de forma tal que constituyan condición suficiente para la verdad de B, donde Γ representa el conjunto de leyes y condiciones iniciales "relevantes" para obtener B. Se constata fácilmente el siguiente problema: cómo identificar el subconjunto Γ de enunciados verdaderos que junto con el antecedente A garanticen la verdad del consecuente B.
Chisholm dio algunos criterios para seleccionar al subconjunto Γ. Entre tales condiciones propuso que las oraciones verdaderas que componen Γ deban ser lógicamente compatibles con el antecedente de dicha expresión condicional, puesto que de otro modo el condicional se tornaría trivialmente verdadero. Sin embargo, debemos observar que la compatibilidad lógica no es condición suficiente, puesto que los siguientes contrafácticos podrían ser ambos verdaderos:
(a) Si hubiera raspado el fósforo, entonces se habría encendido.
(b) Si hubiera humedecido el fósforo, entonces no se habría encendido.
El antecedente de (a) y el de (b) resultan ser lógicamente compatibles, sin embargo parece indeseable la posibilidad de añadir el antecedente de (b) al de (a), dado que ambos implican contrafácticamente enunciados contradictorios. Según Goodman lo que ocurre aquí es que los antecedentes de los mencionados condicionales no resultan ser cosostenibles, i.e., no pueden sostenerse simultáneamente. De ahí que Goodman cambie la formulación primitiva por la siguiente:
"Si A entonces B es verdadero si y sólo si B es derivable a partir de A junto con el conjunto de todas las leyes físicas y todas las proposiciones verdaderas cosostenibles con A."
Es decir, "Si A entonces B" es verdadero si y sólo si B es derivable a partir de A junto con el conjunto de todas las proposiciones verdaderas tales que ninguna de ellas implique contrafácticamente la negación de A y que la negación de algún miembro de ese conjunto sea contrafácticamente implicado por A. Obviamente este enfoque se vuelve circular, dado que la contrafacticidad es definida en términos de la cosostenibilidad y esta última apelando a la primera, consecuencia esta reconocida por el mismo Goodman. Finalmente, resulta interesante observar que la teoría de la derivabilidad, no se formuló bajo la forma de un sistema lógico, pero que intuitivamente parece dar una versión bastante adecuada del Test de Ramsey y ajustarse a la filosofía empirista que el mismo Ramsey compartía, ya que había sido uno de los miembros adherentes más jóvenes del Círculo de Viena.
La creación por parte de Kripke de la semántica de mundos posibles, abrió un nuevo tratamiento para los condicionales contrafácticos. A nuestros propósitos y por razones de simplicidad, nos referiremos solamente al sistema C2 de Robert Stalnaker expuesto en A Theory of Conditionals de 1968. En este trabajo, Stalnaker argumenta explícitamente a favor de la posibilidad de asignar condiciones de verdad a los enunciados condicionales a partir de la sugerencia de Ramsey, dando la siguiente versión del test:
"Primero, agregue (hipotéticamente) el antecedente a su stock de creencias; segundo, realice los ajustes requeridos para conservar la consistencia (sin modificar la creencia hipotética en el antecedente); finalmente, considere si el consecuente resulta verdadero o no".
Parte de reconocer que el TR sólo cubre el caso en el que los hablantes no tienen opinión formada sobre la verdad del antecedente y se pregunta si es posible su generalización. Obviamente no encuentra problemas para el caso en el que el antecedente sea creído como verdadero por el agente, ya que éste podrá agregarlo al stock de creencias sin necesidad de hacer ningún cambio en él. Pero, si el agente considera que el antecedente es falso, al sumarlo a sus creencias generará un conflicto pues deberá introducir algún tipo de cambio en su conjunto de creencias. Stalnaker considera este tipo de consideraciones constituyen la problemática pragmática de los enunciados condicionales y que por lo tanto, si se quiere que las condiciones de verdad de un enunciado condicional sean una función de sus elementos componentes, éstas no deben formularse respecto de contextos particulares de creencias. Por ello, transforma las condiciones de creencia en condiciones de verdad. Su sistema lógico C2 es una extensión de la lógica modal clásica e introduce una nueva conectiva condicional, ">" para representar cualquier tipo de condicional, en particular los condicionales contrafácticos. Las semánticas de Kripke serán su ayuda y el concepto de stock de creencias hipotéticas será reemplazado por el correspondiente de mundo posible.
La semántica de Stalnaker respecto de su sistema C2 de lógica condicional consiste en una estructura <K,ℜ ,λ> donde K es el conjunto de mundos posibles k1,k2,...,Kn.; ℜ es una relación de accesibilidad entre mundos posibles y λ es el mundo absurdo (inaccesible para cualquier mundo posible), y en el cual son verdaderas todas las contradicciones y sus consecuencias lógicas; a la que se agrega una función de selección ƒ que selecciona en el conjuntos de mundos posibles el mundo en el que el enunciado antecedente del condicional es verdadero.
Así surgen las siguientes condiciones de verdad para un enunciado condicional:
A>B es V en ki si B es V en ƒ(A, ki ) y
A>B es F en ki si B es falsa en ƒ(A, ki)
Nuevamente aquí se presenta el problema no lógico de cómo seleccionar el mundo en el que el antecedente del condicional sea verdadero y que Stalnaker "soluciona" poniendo condiciones a la función de selección f que a nuestro objeto no es necesario reproducir. Lo que sí interesa a nuestros propósitos es mostrar que se satisfacen las condiciones originales (i)-(iii) del TR. En efecto, a partir de esta semántica y los axiomas dados del sistema C2, la conectiva > es caracterizada formalmente como intermedia entre el condicional estricto y el condicional material, de tal forma que cuando el antecedente A del enunciado A>B es verdadero en el mundo actual ki, se reduce a un condicional material y, cuando el antecedente es falso en el mundo actual ki, puede darse o bien que el consecuente del condicional resulte verdadero en el mundo seleccionado Kj, en cuyo caso el enunciado condicional A>B es verdadero en el mundo actual ki; o bien que el consecuente del enunciado condicional sea falso en el mundo seleccionado Kj y el enunciado A>B sea falso en el mundo actual ki.
Tanto el sistema C2 de Stalnaker como el VC de D. Lewis y, en general todas las lógicas condicionales normales, satisfacen la propiedad de Monotonía de la relación de deducibilidad formulada en el metalenguaje, formalmente:
Si Γ A entonces Γ ∪{B} Δ Monotonía
Esta propiedad garantiza que el Test de Ramsey se satisfaga ya que en el mundo seleccionado para validar el condicional A>B sólo se puede inferir B si se ha dado A, i.e, que el condicional material sea verdadero en el mundo seleccionado. Asimismo, de acuerdo al requisito (iii), se constata fácilmente que TR implica monotonía. Sin embargo, debemos observar que el condicional > no satisface en el lenguaje objeto las siguientes propiedades:
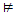(A > B) → ((A∧C) >B) Refuerzo del Antecedente (RA)
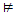((A > B) ∧ (B >C))→ (A >C) Transitividad (TRN)
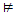(A > ¬B) → (B > ¬A) Contraposición (CT)
Y que, si RA no se cumple, i.e., que el agregado de una oración al antecedente de un condicional no preserva la verdad del consecuente, pese a que la noción de consecuencia es monótona, la conectiva > es un condicional "derrotable" o revocable, como puede notarse claramente en la siguiente sucesión de condicionales contrafácticos:
Si hubiera raspado el fósforo se habría encendido.
Si hubiera raspado el fósforo y este hubiera estaba húmedo, no se habría encendido.
Si hubiera raspado el fósforo y este hubiera estado húmedo pero hubiera esperado a que se secara, entonces se habría encendido.
Etc. etc.
Si bien los sistemas condicionales citados satisfacen el TR, ellos lo hacen habiendo sacrificado las condiciones (i) y (ii), o sea, despojando al TR de su enfoque epistémico original y no tomando en cuenta ni el stock de creencias del hablante ni la petición de que, a fin de evaluar un enunciado condicional, el antecedente deba adicionarse al stock creencias previas, contemplándose la posibilidad de que al adicionarse el antecedente, sea posible que deba realizarse algún ajuste para compatibilizar la nueva creencia con el conjunto de las creencias viejas. Estas observaciones llevaron a una nueva versión del TR en términos de sistemas de creencias. Una de las más conocidas es la creada por Carlos Alchourrón, David Makinson y Peter Gärdenfors (AGM debido a las iniciales de sus autores). 2
En AGM se parte de un conjunto K de creencias de un agente racional, el cual se supone es consistente y cerrado bajo la noción de consecuencia lógica clásica y al cual se le suman tres clases de postulados que caracterizan tres tipos de cambios epistémicos representados por operaciones sobre el conjunto K, a saber: los postulados de expansión del conjunto K, o sea los que caracterizan como el conjunto K se expande cuando se agrega una nueva creencia p consistente con K; los postulados de contracción, o sea los que caracterizan los cambios que se producen en K cuando una creencia particular p es extraída del conjunto de creencias del hablante y los postulados de revisión,los cuales describen los cambios que se producen en K cuando se agrega una nueva creencia p que no es consistente con las antiguas de K. Evidentemente, esta perspectiva parece adecuarse al enfoque de Ramsey presentado y la operación de revisión parece ser la adecuada para representar particularmente el requisito (ii). En efecto, mediante la operación de revisión, denotada por *, Gärdenfors da la siguiente versión del Test de Ramsey:
p > q ∈ K sii q ∈ K ∗ p.
En palabras, p>q es afirmado respecto de un conjunto de creencias K si y solo si q es implicado por K*p, o sea por el conjunto que ha resultado de "ajustar" o revisar el conjunto K, produciendo en K el mínimo cambio a fin de aceptar el agregado de la creencia p. Es decir K*p representa el mínimo cambio realizado en K a fin de que q pueda incorporarse como nueva creencia preservando consistencia. A fin de comprender esta versión del TR, daremos un ejemplo. Supongamos que Pedro cree (o sabe) que Kennedy fue asesinado y que Oswald fue su asesino y que además era un maniático solitario. Sobre la base de estas creencias, Pedro también cree en la verdad del condicional Si Oswald no hubiera asesinado a Kennedy, entonces Kennedy habría terminado exitosamente su período presidencial. Posteriormente se le informa que se ha descubierto que en realidad existía un complot para su asesinato. Esta información entra en colisión con su creencia anterior de que Oswald era un maniático solitario y por lo tanto sus creencias deben ser revisadas y ahora extraerá la conclusión: Si Oswald no hubiera asesinado a Kennedy, entonces otro lo habría hecho y Kennedy no habría terminado su mandato. Se constata fácilmente que la operación de revisión no es monótona, ya que el agregado de la nueva información ha alterado la aceptabilidad de la conclusión. Hemos llegado así a resultados conflictivos, por un lado, la versión del TR mediante la operación de revisión parece representar fielmente el requisito (ii); por el otro, habíamos afirmado que el TR implica monotonía y3, por último, ahora decimos que la operación de revisión es no-monótona. En efecto, el mismo Gärdenfors se encargó de demostrar un teorema, conocido como teorema de imposibilidad, según el cual el TR sólo se cumple para revisiones triviales, o sea para los casos en que la revisión es nula, i.e., se haga por una oración consistente con el conjunto original K, colapsando así con la expansión. En la literatura actual, dada la importancia que ha tenido AGM tanto en I.A. como en el campo jurídico normativo, se sigue aún investigando sobre el tema variando las propiedades de la operación de revisión o introduciendo otro tipo de operador de revisión a fin de satisfacer por esta vía al TR. Pese a ello, otros lógicos, Gabbay, Krauss, Lehmann y Magidor o Makinson 4 mismo, emprendieron una tarea alternativa para el tratamiento de los enunciados condicionales que consistió en explorar la noción de consecuencia de los llamados condicionales derrotables, involucrados en el ejemplo que dimos para ilustrar la operación de revisión y formularon la actualmente conocida como Teoría de la consecuencia no monótona, la cual intenta dar cuenta del conjunto de las inferencias derrotables o plausibles y desde ella dar un tratamiento para los condicionales. Pero, dado que TR y Monotonía se covalidan y esta relación de consecuencia es no monótona, el TR no se satisface.
Pese a ello, interesa a nuestros fines señalar que esta teoría se construye sobre la noción de consecuencia clásica (i.e., es supraclásica) y a la cual se agregan reglas específicas tales como:
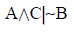
Las tres primeras son básicas a la noción de consecuencia no monótona y la regla 4 es opcional y se adiciona según el tipo de inferencias condicionales que se desee formalizar y a la que hemos incluido porque aludiremos a ella después.
Pasemos ahora a la presentación central de este trabajo, o sea al enfoque propuesto por G. Gocco y L. Fariñas del Cerro en el trabajo Structure, Consequence Relation and Logic (1994) en el cual los autores pretenden generalizar el cálculo de secuentes de Gentzen a las lógicas condicionales, mientras que nosotros trataremos de analizar su comportamiento respecto del Test de Ramsey.
Señalaremos a continuación las ideas previas sobre las que se fundamenta este enfoque:
1) La aplicación de la lógica a las ciencias de la computación requiere, por un lado, de estructuras de información con mayor poder expresivo que las clásicas, en las que se pueda, por ejemplo, tener en cuenta el contenido implícito de algunas oraciones, y por el otro, de un mecanismo estricto de control para la composición de pruebas a fin de no generar inconsistencias;
2) Las lógicas subestructurales (i.e, aquellas que carecen al menos de una regla estructural) tienen la ventaja de que han sido pensadas para manejar distintos tipos de objetos (oraciones, acciones) de forma tal que sus reglas especifican cómo se comportan las conectivas respecto de esos objetos. En síntesis, una lógica puede verse como sistema de razonamientos sobre estructuras particulares de datos con una relación de deducibilidad y un conjunto de reglas de operación en el lenguaje objeto y donde la elección de la estructura depende de las propiedades particulares de los objetos en cuestión.
3) Las reglas estructurales del Cálculo de Secuentes clásico (CS) pueden clasificarse en dos tipos: las data-rules (Contracción y Permutación tanto en el pro como el postsecuente), que definen la estructura fundamental de los objetos a tratar y las reasoning-rules (Identidad, Atenuación en el pro y post secuente y Corte) que definen la relación de deducibilidad, a las cuales se agregan las logical-rules (u operatorias en la terminología usual) que definen las operaciones que se pueden realizar sobre los objetos.
4) Identidad y Corte son las mínimas exigencias que debe cumplir un sistema para ser considerado una lógica.
5) La regla de Corte desempeña en la lógica clásica, el rol fundamental de permitir la composición de pruebas y por lo tanto, a fin de evitar inconsistencias, en muchos casos deberán establecerse restricciones para su uso mediante herramientas lógicas, como lo muestra el siguiente ejemplo:
Supóngase que un agente afirme: (i) A, H1 ├ B y (ii) B, H2 ├ C (donde A, B, H1, H2 son estructuras de información que permiten deducir B y C respectivamente). Supóngase además que H1 y H2 son informaciones implícitas, o sea que no podemos expresar su contenido. Por lo tanto, por Corte es posible obtener el resultado A, H1,H2 ├ C, sin tener en cuenta si H1 y H2 son compatibles. 5
La idea básica de los autores consiste en los siguientes pasos: Primero, introducir un operador condicional contrafáctico (A⇒B) el cual expresa en el lenguaje objeto la relación de deducibilidad A, H ├ B, la cual afirma que hay una deducción de B a partir de A y una hipótesis (o supuesto) H no especificado, que es la que fija el contexto e impide la combinación irrestricta con otros contextos. Segundo, tomando como presentación más adecuada para los enunciados condicionales la sugerida por la Teoría de la Derivabilidad de Chisholm y Goodman, formular un cálculo de secuentes para lógicas condicionales (CSC) utilizando secuentes de segundo grado, i.e., secuentes que pueden poseer dos clases de relación de deducibilidad: una relación de deducibilidad principal, representada por ├P, y una relación de deducibilidad auxiliar, representada por ├α que conformará los secuentes auxiliares, en los cuales se expresarán las restricciones para la composición de pruebas. Para ambos tipos de secuentes, hay operaciones estructurales y lógicas.
Las innovaciones 6 de esta presentación consisten en: (1) los secuentes principales pueden tener conjuntos de fórmulas (como en caso clásico) o, exclusivamente, una sucesión de secuentes auxiliares tanto en el pro como en el post secuente, como por ejemplo:
{A1├α B1},..., {An├αBn} ├P {C1├αD1},...,{Cn ├αDn}
(2) contiene reglas que permiten pasar del nivel clásico al nivel auxiliar reemplazando las fórmulas de los secuentes clásicos por secuentes auxiliares, como en el ejemplo siguiente:
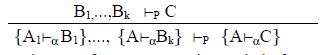
Y (3) Se permite transformar expresiones de la forma {F├αK} en F⇒K.
Sin embargo, debe observarse que, dada la correspondencia entre la relación de deducibilidad ├α y el operador contrafáctico ⇒, la primera no puede ser transitiva. Surge entonces el siguiente problema: Dado que Transitividad y Corte se covalidan, y Corte es la responsable de la identificación de fórmulas en contextos diferentes, Corte debe ser reemplazada por otras reglas que permitan la identificación de fórmulas en las deducciones.
A los efectos de simplificar la exposición, expondremos de manera informal el sistema CO* que es, según los autores la mínima lógica condicional que contiene todos los axiomas e inferencias de la lógica clásica más los siguientes axiomas y reglas:
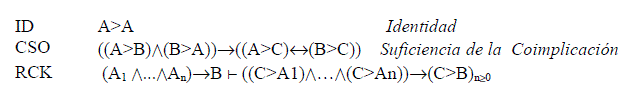
Si se quiere extender esta lógica a los sistemas vistos por nosotros anteriormente, i.e., el sistema C2 de Stalnaker y el VW de D. Lewis, se deberían, agregar al menos el axioma común a ambos:
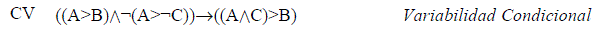
Pasemos ahora a mostrar las reglas del nivel auxiliar, en las que las letras mayúsculas latinas (A,B, C) son fórmulas de LCO*; las mayúsculas griegas (Γ,Δ,Ω) representan el prosecuente y post secuente de las secuencias principales; y las letras mayúsculas latinas (X,Y,Z) representan son los conjuntos que conforman el pro y postsecuente de las secuencias auxiliares.
1. Para los secuentes principales que no contienen secuencias auxiliares, valen las reglas del cálculo de secuentes clásico, i.e, SC, más:
Prefijar (PF)
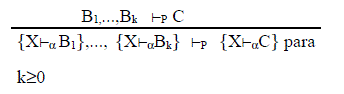
La cual permite realizar lo mostrado en (2) y fijar el contexto en la información implícita de las secuencias auxiliares. Para los secuentes principales que contienen secuencias auxiliares valen las siguientes reglas:
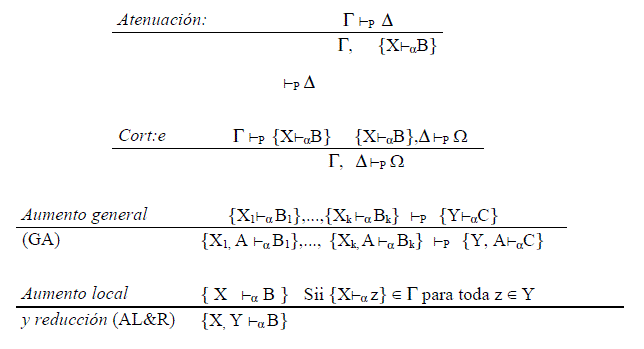
donde Γ es el prosecuente del secuente principal en el cual aparece la premisa de la regla.
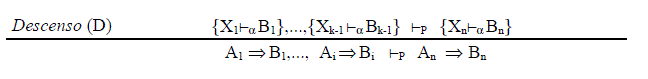
Veamos ahora tres deducciones en CO*:
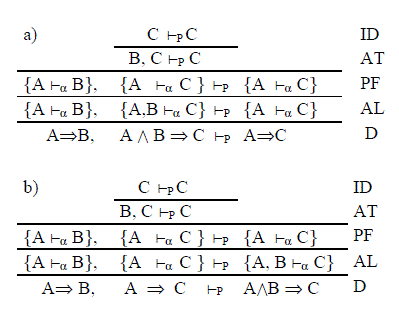
Si se reemplaza el signo ⇒ por el correspondiente a la noción de consecuencia no monótona, podrá comprobarse que se han obtenido las propiedades de Transitividad Cumulativa (a) y Monotonía Cautelosa (b) de esa consecuencia.
Más aún, los sistemas condicionales de C2 de Stalnaker y V de Lewis comparten como axioma la fórmula CV el cual restringe el refuerzo del antecedente a fin de preservar consistencia. Es posible derivar este axioma en CO* y se constatará que coincide con la propiedad de Monotonía Racional de la relación de consecuencia no monótona:
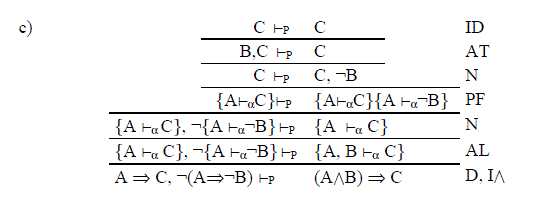
Finalmente debemos preguntarnos dónde ha quedado del Test De Ramsey. Este se satisface en las secuencias principales ya que la relación ├p es monótona, mientras que el conjunto de hipótesis Γ o conocimiento hipotético implícito se refleja en las secuencias auxiliares de acuerdo a la cita (b) del comienzo y que, en tanto procedimiento no monótono, parece acordar formalmente con la función de revisión de AGM y y con la idea intuitiva de revisión del mismo Ramsey.
Chisholm, R.M. (1946) Contrary-to-fact conditionals, en Mind, 55, 289-307. Goodman, N. (1947), The Problem of Counterfactual Conditionals, en Journal of Philosophy , 44, pp. 113-128. Ramsey, F.P.,(1931). The Foundations of Mathematics, London Routledge & Kegan Paul. Ramsey, F.P. (1990). Philosophical Papers, Cambridge University Press. Stalnaker, R. (1975). A Theory of Conditionals, en Causation and Conditionals, Ed.
E. Sossa, Oxford University Press (Primera edición,1968). Crocco, G. y Fariñas del Cerro, L. (1994), Structure, Consequence Relation and Logic, en Crocco y Fariñas del Cerro (Eds) Conditionals: from Philosophy to Computer Science, Clarendon Press, p 239-259.
__________
1 Trabajo leído en las V Jornadas Departamentales de Filosofía (UNLP, 2004).
2 Para consultar una versión completa de una teoría racional del cambio de creencias se recomienda el libro de Gardenfors, P.(1988). Knowlwdge in Flux: Modeling the Dynamics of Epistemic System. The MIT Press-Bradford Books.
3 Para demostrar que TR implica monotonía, se parte de formular monotonía de la siguiente forma: Para todo K y K', y toda oración A, si K⊆ K' entonces K*A ⊆ K'*A
4 Una mayor información en lógicas condicionales y lógica no monótona se encuentra en el texto G.Palau y colaboradores, Lógicas condicionales y razonamiento de sentido común, Gedisa-F.F.y L. (UBA), 2004.
5 Los autores consideran dos mecanismos de control: extra lógicos, que presuponen la identificación de subconjuntos específicos, o los lógicos, que presuponen sólo herramientas lógicas.
6 Los autores reconocen haberse inspirado en el Artículo de Kosta Dosen "Sequent systems for modal logic". The Journal of Symbolic Logic, 50,149-168, 1985.
Esta obra está bajo licencia
Creative Commons Atribución-NoComercial-SinDerivadas 2.5 Argentina